Iris Twist

Iris Twist is a paper folding technique taken from the old fashioned Iris Folding technique from Europe. My intentions were to make this complicated and fabulous form of art something that stampers could use in their card making. So the steps are simplified to make this project demonstrable and repeatable. If you can fold paper and count, you can do this, really!

Supplies

Step-by-Step

1. Step 1

   Take the Iris Pattern and apply some Repositionable Adhesive to the outside of the top of the box. Position the orange cardstock over the pattern so the pattern of the square shows through the cutout of the square in the cardstock. Press down so the repositionable adhesive holds the cardstock to the pattern.
   
   Important note: We are working on the BACK of the finished design, so things may look messy from the back but they will look nice when we turn it over in the end. Trust me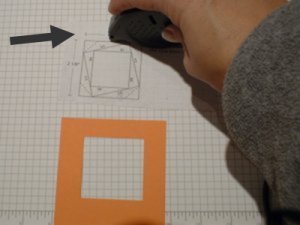
   

   

2. Step 2

   Fold the strip of designer paper in half the long way.
   

   

3. Step 3

   Open the fold and apply Glue Stick adhesive to the inside of this folded paper.
   
   

   

4. Step 4

   Press the fold down so the strip glues itself together...rub a little to get the glue stick to take hold.
   

   

5. Step 5

   Repeat this on the second strip of designer paper so you have two strips.
   
   Note: Don't worry a lot about how well the raw edges of the fold line up, that part will not be seen. The folded edge is the part that will be seen.
   
   

   

6. Step 6

   Apply gluestick adhesive on the orange cardstock around the frame of the opening...keeping the glue on the cardstock only and not on the pattern piece!
   
   
   

   

7. Step 7

   Take your first designer paper strip holding the folded edge facing in towards the center. This will be our '"A" piece. Line the folded edge of this strip up with the slanted line marked by the pattern as "1A". So you are using the lines of the pattern to show you where to place each strip, but the strips only get glued to the cardstock, not to the pattern! For now ignore the dotted lines in each corner of the pattern. See the optional instructions at the end of these directions for working with more than 2 strips of colori>
   
   
   

   

8. Step 8

   Trim the strip off so that we can continue to use that same piece.
   

   

9. Step 9

   You will need to add a little bit of gluestick to the end of that first strip so that...
   

   

10. Step 10

    ...when you line the designer paper strip up for "2A" it will stick where it overlaps on that first piece. Each time you layer on a new strip you will need a little bit of glue on the previous piece.

    

11. Step 11

    Continue the same process around the square for "3A"...
    

    

12. Step 12

    ...and for "4A". You should have enough of this strip to make all four of these pieces.
    

    

13. Step 13

    Apply adhesive to the square created by the first ("A") strip so that the next strip can have something to stick to, once again only apply adhesive to the layers of designer papers and not on the pattern!
    

    

14. Step 14

    Take the other strip of designer paper, this will be the "B" strip. You will complete the same process by gluing onto "5B"...
    

    

15. Step 15

    ...then "6B"...

    

16. Step 16

    ....then "7B".
    
    Now the fun part! Carefully pull the cardstock up off the pattern. The repositionable adhesive allows the pattern to be removed cleanly from the cardstock.
    
    Viola! Your Iris Twist Paper Folding design is done! Remove any remaining adhesive from the front of the cardstock.
    
    Adhere your stamped artwork of choice into the open square to make a nice cardfront design. Take this piece, layer it onto a card and embellish to your hearts content!
    
    

    

17. Finished card.

    

Variations

Another twist
This pattern can incorporate 3 different designer patterns. Start with 3 strips of coordinating designer papers. When you start layering on the strips do not start with "1A" but instead use the dotted lines in each corner first.

Once you have one small piece attached to each of those dotted lines take your second strip of color and complete "1A - 4A" and your third strip to complete "5B - 8B". Enjoy this "Twist" of the Iris Folding technique!

Use your scraps!
If you fold carefully you can also use vellum papers for a very elegant look - a great way to use up those scraps of designer papers!

Your Turn

You've seen the tutorial, now you try it! We've got a section of the gallery set aside for Iris Twist. Try this technique, then upload your artwork to the gallery. Show us your creations!

***Please note - Internet Explorer/Edge is not a supported browser, and will not allow you to see the videos. Please use Chrome, Firefox or Safari to view our tutorial videos.